2025/7/14,
Hiizu Nakanishi
スリンキー・コイルの落下運動のノート
自然長がゼロでバネ定数 $K$、質量 $M$ のバネを $N$ 分割して、
シミュレーションする。
一つのユニットのバネ定数 $k$、質量 $m$ は
\[
k=KN, \qquad m={M\over N}
\]
と与えられる。
鉛直方向上向きに座標軸$z$をとり、バネを吊るす上端を$z=0$、
上から$i$番目のユニットの座標を$z_i$とする。
落下時の運動方程式:
スリンキー・コイルはバネが質量を持っているが、
$N$ 分割した質点がバネ定数 $k$のバネで繋がれていると考える。
上から $i$ 番目の質点の位置 $z_i$ を用いて、
重力と線形バネの力のみを入れた運動方程式は
\begin{align*}
m\ddot z_1 & = -mg - k(z_1-z_2), \\
m\ddot z_i & = -mg -k(2z_i - z_{i-1} -z_{i+1})\,;\qquad i\in [2, N-1],
\\
m\ddot z_N & = -mg -k(z_N-z_{N-1})
\end{align*}
と表される。しかし、これをこのまま解くと、
自然長がゼロなのでバネが縮んだ際に質点の順序が反転する。
バネが縮んだときのコイルの非弾性衝突の効果を簡便に取り入れるために、
質点の順序が入れ替わったとき、すなわち、$z_i > z_{i-1}$となったと
きに、バネの復元力を指数関数的に大きくするとともに、
それに加えて$v_i > v_{i-1}$のときには
比例係数 $\gamma$ で相対速度に比例した散逸を入れる。
すなわち、$i$番目のユニットが$i+1$番目のユニットから受ける力$f_{i, i+1}$を
\begin{align*}
f_{i,i+1} & = \textcolor{red}{H(z_{i, i+1})}\big(-k\,z_{i, i+1}\big)
\\
& \qquad
+ \textcolor{red}{H(-z_{i, i+1})}
\textcolor{blue}{\big( e^{-z_{i, i+1}/w} -1\big)}
\big(k\,w \textcolor{blue}{-\gamma\, v_{i, i+1} }
\textcolor{red}{H(-v_{i, i+1})} \big)
\end{align*}
とした。ただし、$\gamma$ は散逸パラメータで、$w$ はユニットの幅程度
の大きさの長さ、$z_{i, i+1}$ および $v_{i, i+1}$はユニット $i+1$ に対す
るユニット $i$ の相対位置および相対速度で、
\[
z_{i, i+1} = z_i - z_{i+1}, \qquad v_{i, i+1} = \dot z_i - \dot z_{i+1}
\]
である。また、$H(x)$は階段関数:
\[
H(x) = \left\{\begin{array}{ll} 1\qquad & (x\ge 0) \\ 0 & (x<0)
\end{array}\right.
\]
これらを用いて、落下時の運動方程式は、
\begin{align*}
m\ddot z_1 & = -mg + f_{1,2}, \\
m\ddot z_i & = -mg + f_{i,i+1} - f_{i-1,i}\,;\qquad i\in [2, N-1],
\\
m\ddot z_N & = -mg - f_{N-1, N}
\end{align*}
と表される。
釣り合い状態
上端を吊るした釣り合い状態の、
上から$i$番目のユニットの下端の座標 $z^0_i$を求める。
$i$番目のユニットにかかる張力は、そのユニットの重さを無視すれば、
$m\big(N-i\big)g$なので、
その伸び$\Delta z_i$は、
\[
\Delta z_i = {mg\over k}\big( N-i\big)
\]
と与えられる。 $i$番目のユニット下端の座標$z^0_i$は
\[
z^0_i = -\sum_{j=1}^i \Delta z_j
= -{1\over 2}\,{mg\over k}\, i\big( 2N-1-i\big)
\]
となる。これを用いて、コイル全体の長さが
\[
L_g = -z^0_N = {1\over 2}\,{Mg\over K}\, {N(N-1)\over N^2}
\quad\to\quad {1\over 2}\,{Mg\over K} \qquad (N\to\infty)
\]
と得られる。
重心の位置$z^0_G$は、
\[
z^0_G = \sum_{i=1}^N {z^0_{i-1}+z^0_i\over 2N}
= -{M g\over K} {(N+1)(4N-1)\over 12N^2}
\quad\to\quad -{1\over 3}\,{Mg\over K} \quad (N\to\infty)
\]
となる。
$N$が十分大きいとして、
コイルの各部分を$[0,1]$の連続変数 $\ell = i/N$で指定すると、
上端をつるされたコイルの釣り合い状態は、
\[\textcolor{blue}{
z^0(\ell) = z^0_{N\ell}
= -{1\over 2}\,{M\over K}\, g\, \ell\big(2-\ell\big)}\,;
\quad \ell\in[\,0,\,1\,]
\]
で与えられる。
スリンキー・コイルの上端の落下速度
釣り合い状態にあるスリンキー・コイルがその上端を離されて落下するとき、
コイルの各部分はコイルの上端が落ちてくるまで釣り合い状態のまま静止していて、
上端がそこに達したとたん落下部分に取り込まれて、
一緒に落ちてゆくとしよう。
その過程におけるコイルの上端の落下速度の時間変化を求める。
時刻 $t$ で $\ell_{\rm top}(t)=i/N$
までコイルの上端が落ちてきて重なり合ったとする。
その瞬間のコイル全体の重心位置 $z_G(t)$ は、
$z^0\big(\ell_{\rm top}\big)$ で重なり合っている部分の質量が
$\ell_{\rm top}M$ なので、
\begin{align}
z_G(t) & = {1\over M}\left(
\ell_{\rm top}M\, z^0(\ell_{\rm top})
+ \int_{\ell_{\rm top}}^1 d\ell' M\, z^0(\ell')\right)
\\
& = -{1\over 2}\,{M\over K}\, g
\left({2\over 3} + \ell_{\rm top}^2 - {2\over 3}\ell_{\rm top}^3\right)
\end{align}
である。コイルの重心は単純に一定加速度$-g$で落ちてゆくので、
\[
z_G(t) = -{1\over 2}\, g t^2 + z_G^0
\]
でなければならないので、これより時刻 $t$ での $\ell_{\rm top}$ の値は
\[\textcolor{blue}{
\ell_{\rm top}^2\left({1-{2\over 3}\,\ell_{\rm top}}\right)
= {K\over M}\; t^2
}\]
より決まる。
上式で決まる $\ell_{\rm top}(t)$を用いて、時刻 $t$ でのコイルの上端の位置は
\[\textcolor{green}{
z_{\rm top}(t) = z^0\big(\ell_{\rm top}(t)\big)
= -{1\over 2}\,{M\over K}\, g\,
\ell_{\rm top}(t)\big( 2-\ell_{\rm top}(t)\big)
} \tag{1}
\]
と与えられ、上端の落下速度は
\begin{align}
v_{\rm top}(t) & = \dot z_{\rm top} = {d z^0\over d\ell}\, \dot\ell_{\rm top}
=
-{M\over K}\,g\, \big( 1-\ell_{\rm top}\big)\,\dot\ell_{\rm top}
\\
& = -g\sqrt{M\over K}\, \sqrt{1-{2\over 3}\ell_{\rm top}(t)}
\end{align}
と与えられる。
ただし、これらの表式は $\ell_{\rm top}\in[0,1]$でのみ有効であることに注意。
これより、落下し始めた瞬間 $t=0$ のコイル上端の落下速度は、
$\ell_{\rm top}=0$を代入して、
\begin{equation}\textcolor{blue}{
v_{\rm top}(0) = -g\sqrt{M\over K}
} \tag{2}
\end{equation}
となる。コイルの上端は $t=0$で有限の速度で落下し始めることが分かる。
また、$v_{\rm top}$の表式から、
上端の落下速度は時間とともにむしろ遅くなることも分かる。
一様な張力 $T$ がかかった時のバネを伝わる波の速さ
重力がなくバネに一様な張力$T$がかかった時の静止状態は、
\[
z_i^0 = \Delta z\times i\,; \qquad \Delta z = {T\over k}
\]
で与えられ、それからのずれを$\delta z$とする:
\[ z_i = z_i^0 + \delta z_i
\]
角振動数$\omega$、波数$q$の波を
\[
\delta z_i = C \sin(q\, i -\omega t)
\]
とすると、分散関係は
\[
\omega^2 = {k\over m}\, 2(1-\cos q) \approx {k\over m}\, q^2
\qquad\mbox{for $q \approx 0$}
\]
と与えられる。これより、
一様な張力 $T$ が加わった自然長ゼロのバネを伝わる波の伝播速度は
\[
v(T) = \sqrt{k\over m}\, \Delta z(T) = {T\over\sqrt{MK}}
\]
と与えられる。特に、張力がバネ全体の重力に一致している時、
すなわち $T=Mg$ の時には、
\begin{equation}\textcolor{blue}{
v(Mg) = g\sqrt{M\over K}
} \tag{3}
\end{equation}
となり、これは上で求めた、
コイルが落ち始めた瞬間の上端の速度(2)に一致している。
つるされたスリンキー・コイルを伝わるパルス
一般に、
釣り合い状態にある線形バネの一端に $t=0$ に外からパルスを加えたとき、
その影響が時刻 $t$ に $i_p(t)$ 番目のユニットまで伝わったとすると、
$i_p(t)$ は
\[
i_p(t) = \sqrt{k\over m}\times t
\]
で与えられる。対応する $\ell_p(t)$ は
\[\textcolor{blue}{
\ell_p(t) = {i_p(t)\over N} = \sqrt{K\over M}\times t
} \]
となり、これによりパスルの伝播が記述される。
鉛直に垂らしたスリンキーコイルの上端にパルスを加えた場合には、
伝播したパルスの先端の座標 $z_p(t)$ は、
\[
\textcolor{green}{
z_p(t) = z^0\big(\ell_p(t)\big)
= -g\sqrt{M\over K}\; t \left( 1-{1\over 2}\sqrt{K\over M}\; t \right)
}\tag{4}
\]
である。
これより、パルスが伝わる速度の時間変化 $v_p(t)$は
\begin{align}
v_p(t) & = {d z_p\over dt}
= -{M\over K}\, g\, \big( 1-\ell_p\big)\, \dot\ell_p
\\
& = -g\left(\sqrt{M\over K} -t\right)
\end{align}
で与えられる。
これらの表式は、パルスがバネの終端に達するまで、すなわち
\[
t < \sqrt{M\over K}
\]
のみ、有効であることに注意。
グラフ
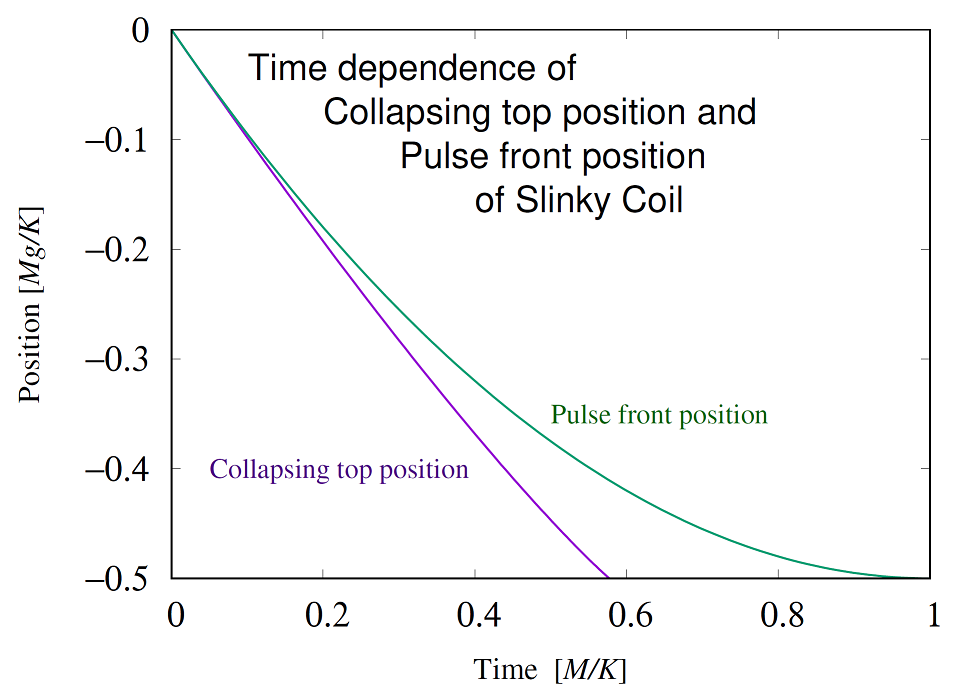
落下するスリンキー・コイルの上端の位置の時間変化(1)と、
吊るしたスリンキーコイルを伝わるパルスの先端の位置の時間変化(4)。
最初は両者は同じ速さだが、コイルの上端のほうが次第に先に落ちてゆくこと
がわかる。