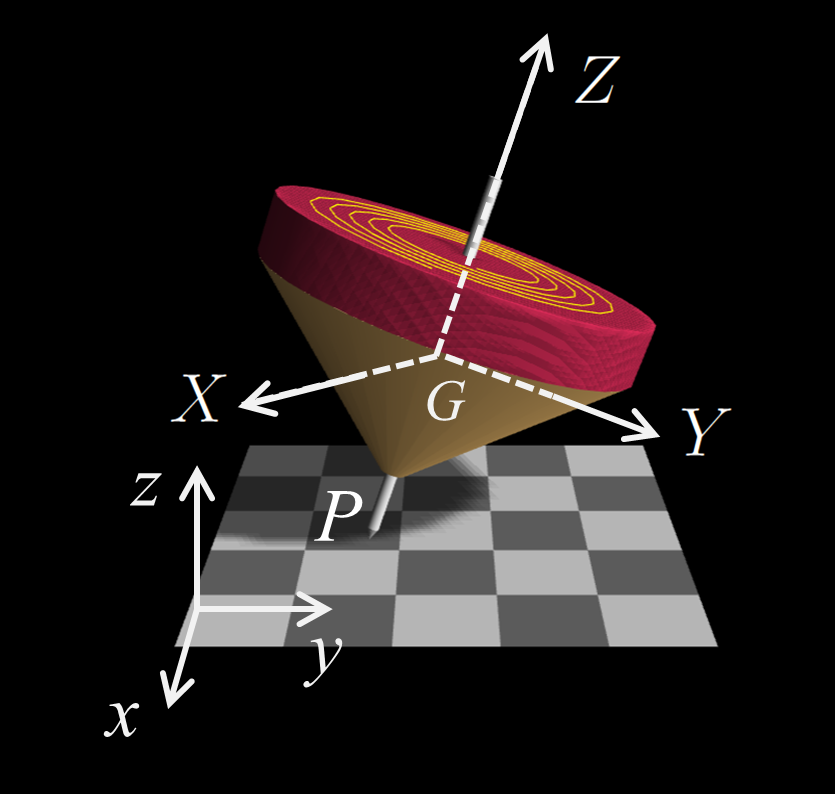
重心の速度$\vec v_G$と重心まわりの角運動量$\vec L_G$の満たす方程式は、 \[\left\{\begin{array}{rl}\displaystyle M{d\vec v_G\over dt} & = -Mg \vec e_z + \vec N \\ \displaystyle {d\vec L_G\over dt} & = \big(-h \vec e_Z\big) \times\vec N \end{array}\right. \] と与えられる。 ただし、$M$はコマの質量、 $\vec N$は軸の先端が床から受ける力、 $g$は重力の加速度の大きさ、 $\vec e_z$は$z$方向(鉛直上向き)の単位ベクトル、 $h$は軸の先端Pとコマの重心Gの間の距離、 $\vec e_Z$はコマの軸に沿った$Z$軸方向の単位ベクトルである。
床からの力$\vec N$は、 床面に平行な摩擦力$\vec F$と垂直抗力$\vec R$からなる: \[ \vec N = \vec F + \vec R; \qquad \vec F \,\perp\, \vec e_z, \quad \vec R =R \vec e_z\,. \] 摩擦力$\vec F$は軸の先端Pの速度$\vec v_P$に比例するとする: \[ \vec F = -k \vec v_P\,. \] ここで、$k$は抵抗(まさつ)係数。
一方、垂直抗力$R$は、軸の先端$P$が床面から離れない条件から決まる。 すなわち、$\vec v_P$が$xy$面内にある条件 \[ \vec v_P \cdot \vec e_z = 0\,;\qquad \vec v_P = {d\over dt}\big( \vec r_G -h\vec e_Z\big) = \vec v_G - h\vec\omega\times\vec e_Z \] より、重心の速度$\vec v_G$はコマの角速度$\vec\omega$を用いて表され、 それを$\vec v_G$の運動方程式の$z$成分に代入することにより、 $R$は$\vec\omega$とその時間微分を用いて表される。
シミュレーションに用いた具体的方程式の導出は 計算ノート を見てください。