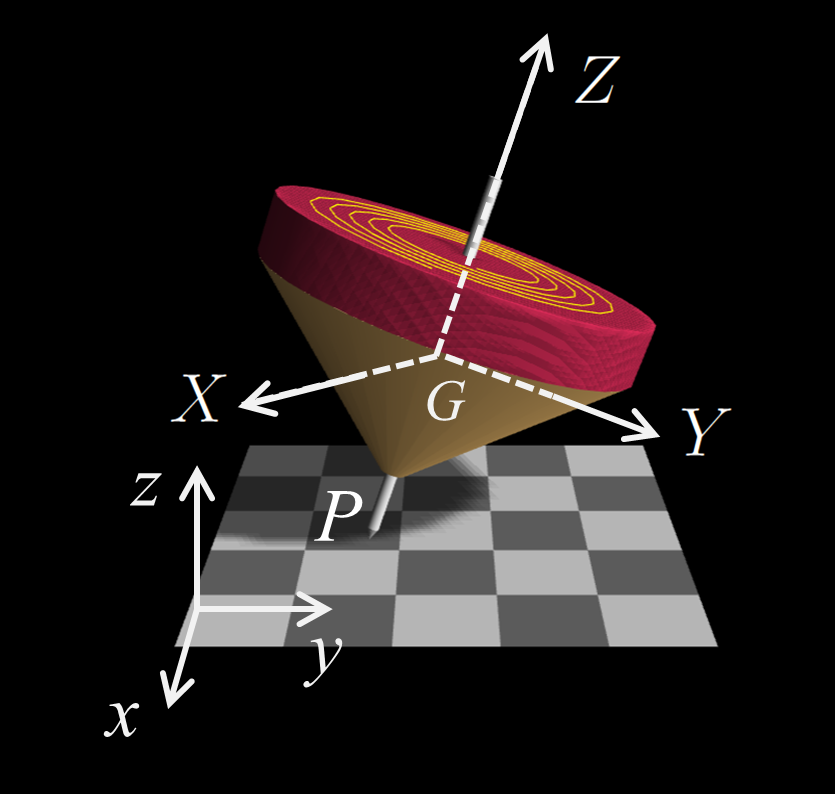
回転軸の先端Pが床を滑る場合の対称コマのシミュレーター。
軸の先端Pは、その速度$\vec v_P$に比例した抵抗力
\[
\vec F = -k \vec v_P
\]
を受けるとします。
軸の先端Pは床の上を滑り、コマは摩擦によってエネルギーを失うので、
軸がだんだんと傾いてゆきます。
しかし、軸は床と一点で接しているとしているので軸回りのトルクはゼロで、
コマのスピン速度$\omega_Z$は減衰せず一定です。
抵抗係数$k$が大きいと軸の先端Pは殆ど動かず、 軸の先端が床に固定された場合のような運動をします。
$k$がゼロの場合は 床からの摩擦力はなく、コマの重心Gが不動となる運動をします。
抵抗係数$k$が大きい場合と、 軸の先端が完全に固定された場合との大きな違いは、 軸が揺らぐ章動が摩擦によって速やかに減衰し、 自然と定常歳差運動に落ち着くことです。
また、先端 P が固定された場合には、 与えられたスピン速度$\omega_Z$と軸の傾き角$\theta$に対して、 低速歳差運動と高速歳差運動の2つの定常歳差運動があるのに対して、 このシミュレーションを見ると、 Pが固定されていない場合には、$k$が大きく軸の先端がほとんど動かなくても、 高速歳差運動は不安定ですぐに低速歳差運動に収束するようです。
軸の先端が固定されていない 実際のコマの運動を観察すると、 高速回転させた場合、 章動だけでなく歳差運動も減衰して、 しばらく直立状態で落ち着くように見えます。 この振る舞いは、このシミュレーターでは観察されません。 その理由は、軸の先端の大きさを無視したところにあるのかもしれません。
