Theory of Foucault Pendulum
The rotational speed of the pendulum’s oscillation plane depends on latitude. At a point of northern latitude $\Theta$ ($0\leqq \Theta\leqq \pi/2$), we want to find the time it takes for the oscillation plane to complete one full rotation. Below, we neglect the revolution of the Earth and assume that the center of the Earth G is stationary.Coordinate System
We take the observation point on the ground as the origin O of a coordinate system fixed to the Earth. The axes are defined such that the $x$-axis points south, $y$-axis points east, and $z$-axis points vertically upward (opposite to the gravity).Let the position of a particle be P, and we examine its motion. In this coordinate system, the position vector of the particle is $\bm r =\overrightarrow{\rm OP} := (x, y, z)$. Let $\bm\omega$ be the angular velocity vector of Earth's rotation, and let $\bm r_0 = \overrightarrow{\rm GO}$ be the vector from the center of the Earth G to the origin O. We now derive the equation of motion of the particle in this coordinate system fixed to the Earth.
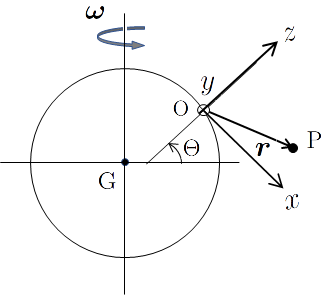
Equation of Motion
Let $\bm r_P := \bm r_0 + \bm r$ be the displacement vector pointing from G to P. Then the velocity $\bm v_P$ and acceleration $\bm a_P$ of the particle at P are: \begin{align} \bm v_P & = {d\bm r_P\over dt} = \bm{\dot r}_P + \bm\omega\times\bm r_P = \bm{\dot r} +\bm\omega\times\big(\bm r_0+\bm r\big) \\ \bm a_P & = {d\bm v_P\over dt} = \bm{\ddot r}+2\bm\omega\times\bm{\dot r} + \bm{\dot\omega}\times\big(\bm r_0 + \bm r\big) + \bm\omega\times\big(\bm\omega\times(\bm r_0+\bm r)\big) \end{align}Here, dots denote time derivatives and for a vector \[\bm A =A_x\bm e_x +A_y\bm e_y +A_z\bm e_z =: (A_x, A_y, A_z),\] the apparent time derivative is written as: \[ \bm{\dot A}:= \big( \dot A_x, \dot A_y, \dot A_z\big) = \dot A_x\bm e_x + \dot A_y\bm e_y + \dot A_z\bm e_z \] where $\bm e_x$, $\bm e_y$, and $\bm e_z$ are unit vectors along the $x$, $y$, and $z$ axes, which rotate with the coordinate system fixed to the Earth. The time derivative is then: \[ {d\bm A\over dt}= \bm{\dot A}+\bm\omega\times\bm A \]
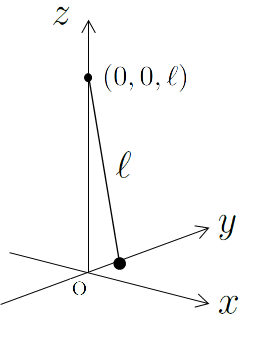
Consider a pendulum with a mass $m$ suspended by a light string of length $\ell$ fixed at the point $(0, 0, \ell)$.
Assuming Earth's rotation does not change over time, we have: \[ {d\bm\omega\over dt} = \bm{\dot\omega}+\bm\omega\times\bm\omega =\bm{\dot\omega} = 0 \]
If the only forces acting on the mass are gravity from the Earth and the tension $\bm S$ of the string, the equation of motion becomes: \[ m\Big(\bm{\ddot r}+2\bm\omega\times\bm{\dot r} + \bm\omega\times\big( \bm\omega\times(\bm r_0 +\bm r)\big)\Big) = \bm S -G{Mm\over \big|\bm r_0+\bm r\big|^3}\big(\bm r_0 +\bm r\big) \] Here, $M$ is Earth's mass and $G$ is the gravitational constant.
The third term in parentheses on the left-hand side is the centripetal acceleration. The corresponding apparent force is the “centrifugal force”. The combined effect of centrifugal and gravitational forces gives the effective gravity: \[ m\bm g = -m\left( \bm\omega\times\big(\bm\omega\times(\bm r_0+\bm r)\big) +{GM\over\big|\bm r_0+\bm r\big|^3}(\bm r_0+\bm r) \right) \] Using this, the equation governing the displacement vector $\bm r$ becomes: \begin{equation} m\big(\bm{\ddot r}+2\bm\omega\times\bm{\dot r}\big) = \bm S+m\bm g \tag{1} \end{equation} Here we assume $r_0 \gg r$ and neglect the $r$-dependence of the gravitational and centrifugal terms, thus we treat $\bm g$ as a constant vector.
Motion of the Particle in the Horizontal Plane
Let us express $\bm\omega$, $\bm S$, and $m\bm g$ in components: \[ \bm\omega = \omega(-\cos\Theta, 0, \sin\Theta),\quad \bm S = -{S\over\ell} (x, y, z-\ell), \quad m\bm g = (0,0,-mg) . \] Substituting into Eq. (1), the components are: \begin{align} m\big( \ddot x -2\omega\sin\Theta\;\dot y\big) & = -S\;{x\over\ell} \tag{2}\\ m\big( \ddot y +2\omega(\sin\Theta\;\dot x+\cos\Theta\;\dot z)\big) & = -S\; {y\over\ell} \tag{3}\\ m\big( \ddot z -2\omega\cos\Theta\;\dot y\big) & = -mg +S\;{\ell -z\over\ell} \tag{4} \end{align}Assuming $\ell$ is much longer than the oscillation amplitude, we neglect motion in the $z$-direction. Substitute $z = 0$ in Eq. (4), then the tension $S$ is: \[ S = mg-2m\omega\cos\Theta\, \dot y \] Using this in Eqs. (2) and (3), we get: \begin{align} \ddot x -2\omega \sin\Theta\,\dot y & = -{g\over\ell}\, x \tag{5}\\ \ddot y +2\omega \sin\Theta\,\dot x & = -{g\over\ell}\, y \tag{6} \end{align} Higher-order terms in displacement and derivatives are ignored.
General Solution of the Equations
Eqs. (5) and (6) are linear ODEs with constant coefficients. We can find the general solution using standard methods. However, a simpler approach is to define a complex variable [Note] : \[ \bm r=\left(\begin{array}{cc} x \\ y \end{array}\right) \qquad\Leftrightarrow\qquad \xi=x + iy \] This maps planar motion to the complex plane. A rotation by angle $\theta$ about the origin corresponds to multiplication by $e^{i\theta}$: \[ \hat R(\theta)\bm r = \left(\begin{array}{cc} \cos\theta\,x -\sin\theta\,y \\ \sin\theta\,x + \cos\theta\, y \end{array}\right) \qquad\Leftrightarrow\qquad e^{i\theta}\xi \]From Eqs. (5) and (6), $\xi$ satisfies: \begin{equation} \ddot\xi +2\omega\sin\Theta\; i\dot\xi + {g\over \ell}\, \xi = 0 \tag{7} \end{equation} The general solution is obtained by the standard method as \[ \lambda^2 + 2\omega\sin\Theta\, \lambda -{g\over\ell} = 0 \quad\Rightarrow\quad \lambda = -\omega_F \pm \omega_g \] \[ \omega_F := -\omega\sin\Theta, \qquad \omega_g := \sqrt{(\omega\sin\Theta)^2 +{g\over\ell}} \] Thus the solution is \begin{equation} \xi = e^{-i\omega_F t}\big( C\,e^{-i\omega_g t} +D\,e^{i\omega_g t}\big), \tag{8} \end{equation} where $C$ and $D$ are arbitrary complex constants.
The term $C\, e^{-i\omega_g t}$ describes clockwise circular motion; $D\, e^{i\omega_g t}$ is counterclockwise. Together, they describe any 2D oscillation about the origin. The factor $e^{-i\omega_F t}$ causes the oscillation plane to rotate clockwise at rate $\omega_F$, thus Eq.(8) shows
An oscillation at angular frequency $\omega_g$ rotating CW at angular speed $\omega_F$
In particular, when $C = D = C_0/2$ (real constant), \[ \xi = e^{-i\omega_F t} C_0 \cos(\omega_g t) \Rightarrow \left\{\begin{array}{rl} x & = C_0 \cos(\omega_g t) \cos(-\omega_F t), \\ y & = C_0 \cos(\omega_g t) \sin(-\omega_F t) \end{array}\right. \] This corresponds to a pendulum whose oscillation plane rotates CW at angular velocity $\omega_F$.
Note: See Landau & Lifshitz, *Mechanics*, §39, Problem 3.