Foucaultの振子の理論
振り子の振動面の回転速度は緯度に依存する。 北緯 $\Theta$ ($0\leqq \Theta\leqq \pi/2$)の地点において, 振り子の振動面が一回転するのにかかる時間を求めたい。 以下では,地球の公転運動は無視し,地球の中心 Gは静止しているものとする。座標系
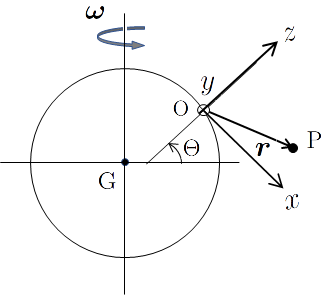
地上の観測地点を座標原点 O とし,地球に固定された座標系を考える。 座標軸は,$x$ 軸を南向き,$y$ 軸を東向き,$z$ 軸を鉛直上向き, すなわち重力と反平行にとる。質点の位置を P として,その運動を考える。 この座標系における質点の位置ベクトルを $\bm r =\overrightarrow{\rm OP} := (x, y, z)$ と表す。 地球の自転の角速度ベクトルを$\bm\omega$, 地球の中心 G から座標原点 O に向かうベクトルを $\bm r_0 = \overrightarrow{\rm GO}$ として, この座標系において質点の運動方程式を導出しよう。
運動方程式
静止点 G からの質点の変位ベクトルを $\bm r_P:=\bm r_0 + \bm r$ として, 点Pにある質点の速度 $\bm v_P$,および 加速度 $\bm a_P$は, \begin{align} \bm v_P & = {d\bm r_P\over dt} = \bm{\dot r}_P + \bm\omega\times\bm r_P %{d\bm r_0\over dt} + {d\bm r\over dt} = \bm{\dot r} +\bm\omega\times\big(\bm r_0+\bm r\big) \\ \bm a_P & = {d\bm v_P\over dt} = \bm{\ddot r}+2\bm\omega\times\bm{\dot r} + \bm{\dot\omega}\times\big(\bm r_0 + \bm r\big) + \bm\omega\times\big(\bm\omega\times(\bm r_0+\bm r)\big) \end{align} と与えられる。ただし,ドットは時間微分を表し,ベクトル \[\bm A =A_x\bm e_x +A_y\bm e_y +A_z\bm e_z =: (A_x, A_y, A_z) \] に対して,その見かけの時間変化率を \[ \bm{\dot A}:= \big( \dot A_x, \dot A_y, \dot A_z\big) = \dot A_x\bm e_x + \dot A_y\bm e_y + \dot A_z\bm e_z \] 等と表記した。ここで,$\bm e_x$, $\bm e_y$, $\bm e_z$ はそれぞれ$x$ 軸, $y$ 軸, $z$ 軸方向の単位ベクトルで、 地球に固定された座標系とともに角速度$\bm\omega$で回転している。 $\bm A$の時間変化率 $d\bm A/dt$ は、これを用いて \[ {d\bm A\over dt}= \bm{\dot A}+\bm\omega\times\bm A \] と表される。
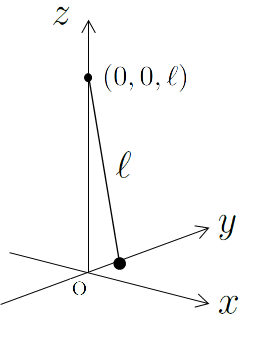
座標 $(0, 0, \ell)$ の点で端点を固定した長さ $\ell$ の軽い紐につるされた 質量 $m$ の質点の振り子運動を考える。
まず,地球の自転は時間変化しないとすると, \[ {d\bm\omega\over dt} = \bm{\dot\omega}+\bm\omega\times\bm\omega =\bm{\dot\omega} = 0 \] である。
質点には地球からの引力と紐の張力 $\bm S$ が働いているとすると, 運動方程式は \[ m\Big(\bm{\ddot r}+2\bm\omega\times\bm{\dot r} + \bm\omega\times\big( \bm\omega\times(\bm r_0 +\bm r)\big)\Big) = \bm S -G{Mm\over \big|\bm r_0+\bm r\big|^3}\big(\bm r_0 +\bm r\big) \] と表される。ただし,地球の質量を$M$,万有引力定数を$G$とした。
左辺括弧中の第3項は向心加速度で, それに由来する見かけの力を「遠心力」と呼ぶ。 遠心力と地球引力との合力である重力は \[ m\bm g = -m\left( \bm\omega\times\big(\bm\omega\times(\bm r_0+\bm r)\big) +{GM\over\big|\bm r_0+\bm r\big|^3}(\bm r_0+\bm r) \right) \] と表される。これを用いて,質点の変位ベクトル$\bm r$の従う方程式は \begin{equation} m\big(\bm{\ddot r}+2\bm\omega\times\bm{\dot r}\big) = \bm S+m\bm g \tag{1} \end{equation} となる。以下では,$r_0\gg r$として, 遠心力および地球の引力の $\bm r$ 依存性を無視し, $\bm g$ は定ベクトルとする。
水平面内での質点の運動
地球の角速度ベクトル $\bm\omega$,紐の張力 $\bm S$,重力 $m\bm g$ を それぞれ成分で表すと, \[ \bm\omega = \omega(-\cos\Theta, 0, \sin\Theta),\quad \bm S = -{S\over\ell} (x, y, z-\ell), \quad m\bm g = (0,0,-mg) \] なので,これを用いて方程式(1)の各成分を書くと, \begin{align} m\big( \ddot x -2\omega\sin\Theta\;\dot y\big) & = -S\;{x\over\ell} \tag{2}\\ m\big( \ddot y +2\omega(\sin\Theta\;\dot x+\cos\Theta\;\dot z)\big) & = -S\; {y\over\ell} \tag{3}\\ m\big( \ddot z -2\omega\cos\Theta\;\dot y\big) & = -mg +S\;{\ell -z\over\ell} \tag{4} \end{align} となる。振り子の振動の振幅に比べて紐の長さ $\ell$ は十分長く, 質点の $z$ 方向の運動は無視できるとして,式(4)で$z=0$を代入すると, 紐の張力$S$は \[ S = mg-2m\omega\cos\Theta\, \dot y \] と与えられ,これを用いて式(2)と(3)は \begin{align} \ddot x -2\omega \sin\Theta\,\dot y & = -{g\over\ell}\, x \tag{5}\\ \ddot y +2\omega \sin\Theta\,\dot x & = -{g\over\ell}\, y \tag{6} \end{align} となる。 ただし,微小振動の近似で変位 $x$, $y$ およびその時間微分の2次の項は無視した。
方程式の一般解
方程式(5),(6)は定数係数の線形常微分方程式なので, 標準的な方法によって一般解を求めることができる。 しかし、この方程式は簡単な構造をしているので、 2次元$x-y$平面と複素平面との対応付け \[ \bm r=\left(\begin{array}{cc} x \\ y \end{array}\right) \qquad\Leftrightarrow\qquad \xi=x + iy \] を用いると、 さらに容易に一般解を求めることができる。 注) この対応付けでは、位置ベクトルの平行移動は複素数の和に対応し、 原点を中心とする角度 $\theta$ の回転は $e^{i\theta}$ との積で表されること、すなわち、 \[ \hat R(\theta)\bm r = \left(\begin{array}{cc} \cos\theta\,x -\sin\theta\,y \\ \sin\theta\,x + \cos\theta\, y \end{array}\right) \qquad\Leftrightarrow\qquad e^{i\theta}\xi \] に注意しよう。 ただし、$\hat R(\theta)$は2次元の回転行列 \[ \hat R(\theta) = \left(\begin{array}{cc} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{array}\right)\; . \]$\xi$の従う方程式は、式(5)および(6)より、 \begin{equation} \ddot\xi +2\omega\sin\Theta\; i\dot\xi + {g\over \ell}\, \xi = 0 \tag{7} \end{equation} となり、これは $\xi = \xi_0\, e^{i\lambda t}$ とおくことによって直ちに解ける。すなわち、特性方程式 \[ \lambda^2 + 2\omega\sin\Theta\, \lambda -{g\over\ell} = 0 \] の解は \[ \lambda = -\omega_F \pm \omega_g\, , \]\[ \omega_F := = -\omega\sin\Theta, \qquad \omega_g := \sqrt{\big(\omega\sin\Theta\big)^2 +{g\over\ell}} \] なので、一般解は \begin{equation} \xi = e^{-i\omega_F t}\big( C\,e^{-i\omega_g t} +D\,e^{i\omega_g t}\big) \tag{8} \end{equation} と求まる。ただし、$C$および$D$は積分定数で任意の複素数。
右辺括弧の第1項$C\, e^{-i\omega_g t}$は角速度$\omega_g$のCWの円運動、 右辺括弧の第2項$D\, e^{i\omega_g t}$は角速度$\omega_g$のCCWの円運動を表し、 この2つの和は原点を中心とする角速度$\omega_g$の任意の2次元振動を与える。 これに因子$e^{-i\omega_Ft}$がかかっているので、 式(8)は
角速度 $\omega_g$ の振動が角速度 $\omega_F$ でCWに回転する運動を表す。
特に、$C=D \equiv C_0/2$ (実数)の場合には、 \[ \xi = e^{-i\omega_F t} C_0 \cos(\omega_g t) \qquad\Rightarrow\qquad \left\{\begin{array}{rl} x & = C_0 \cos(\omega_g t) \cos(-\omega_F t), \\ y & = C_0 \cos(\omega_g t) \sin(-\omega_F t) \end{array}\right. \] となり、 $\omega_g$の振り子の振動面が$\omega_F$でCW方向に回転する運動に対応する。
注) ランダウ・リフシッツ、「力学」、第39節、問題3.