2025/7/14,
Hiizu Nakanishi
Note on the Falling Motion of a Slinky Coil
We simulate a spring of zero natural length with spring constant $K$
and total mass $M$ by dividing it into $N$ segments.
The spring constant $k$ and mass $m$ of each segment are
\[
k = K N, \qquad m = {M\over N}\, .
\]
Taking the vertical $z$‑axis upward, we set the suspension point of
the spring at $z=0$ and denote the coordinate of the $i$‑th
segment from the top by $z_i$.
Equations of motion during free fall
Although a slinky coil is a spring with mass, we model it as $N$ point masses connected by springs of spring constant $k$.
Using the position $z_i$ of the $i$‑th mass from the top, the equations of motion including only gravity and the linear spring forces are
\begin{align*}
m\ddot z_1 & = -mg - k(z_1-z_2), \\
m\ddot z_i & = -mg -k(2z_i - z_{i-1} -z_{i+1})\,;\qquad i\in [2, N-1], \\
m\ddot z_N & = -mg -k(z_N-z_{N-1})
\end{align*}
However, solving these equations as they stand causes the order of the masses to invert when the spring contracts, because its natural length is zero.
To conveniently incorporate the effect of inelastic collisions in the
coil when the spring contracts, we introduce
the restoring force that increases exponentially
when the order of the masses swaps—that is, when $z_i > z_{i-1}$ —
along with a dissipative force proportional to the
relative velocity with coefficient $\gamma$ when $v_i > v_{i-1}$.
Specifically, the force $f_{i,i+1}$ exerted on segment $i$ by segment $i+1$
is set to
\begin{align*}
f_{i,i+1} & = \textcolor{red}{H(z_{i, i+1})}\big(-k\,z_{i, i+1}\big) \\
& \qquad
+ \textcolor{red}{H(-z_{i, i+1})}
\textcolor{blue}{\big( e^{-z_{i, i+1}/w} -1\big)}
\big(k\,w \textcolor{blue}{-\gamma\, v_{i, i+1} }
\textcolor{red}{H(-v_{i, i+1})} \big)
\end{align*}
Here, $\gamma$ is the dissipation parameter, $w$ is a length of the
order of the segment width, and $z_{i, i+1}$ and $v_{i, i+1}$ are
respectively the relative position and relative velocity of segment $i$
with respect to segment $i+1$:
\[
z_{i, i+1} = z_i - z_{i+1}, \qquad v_{i, i+1} = \dot z_i - \dot z_{i+1}
\]
$H(x)$ is the Heaviside step function:
\[
H(x) = \left\{\begin{array}{ll} 1\qquad & (x\ge 0) \\ 0 & (x<0)
\end{array}\right.
\]
Using these, the equations of motion during free fall are given by
\begin{align*}
m\ddot z_1 & = -mg + f_{1,2}, \\
m\ddot z_i & = -mg + f_{i,i+1} - f_{i-1,i}\,;\qquad i\in [2, N-1], \\
m\ddot z_N & = -mg - f_{N-1, N} \, .
\end{align*}
Equilibrium configuration
We determine the coordinate $z^0_i$ of the lower end of the $i$‑th
segment from the top in the equilibrium configuration with the top
being suspended.
Neglecting the weight of its own, the tension acting on the
$i$‑th segment is $m\big(N-i\big)g$, so the extension $\Delta z_i$ is
\[
\Delta z_i = {mg\over k}\big( N-i\big).
\]
The coordinate $z^0_i$ of the lower end of the $i$‑th segment is
\[
z^0_i = -\sum_{j=1}^i \Delta z_j
= -{1\over 2}\,{mg\over k}\, i\big( 2N-1-i\big).
\]
From this, the total length of the coil is obtained as
\[
L_g = -z^0_N = {1\over 2}\,{Mg\over K}\, {N(N-1)\over N^2}
\quad\to\quad {1\over 2}\,{Mg\over K} \qquad (N\to\infty).
\]
The center‑of‑mass position $z^0_G$ is
\[
z^0_G = \sum_{i=1}^N {z^0_{i-1}+z^0_i\over 2N}
= -{M g\over K} {(N+1)(4N-1)\over 12N^2}
\quad\to\quad -{1\over 3}\,{Mg\over K} \quad (N\to\infty).
\]
For large $N$, specifying each part of the coil
by the continuous variable $\ell = i/N \in[0,1]$, the equilibrium
profile of the coil suspended at its top end is given by
\[
\textcolor{blue}{
z^0(\ell) = z^0_{N\ell}
= -{1\over 2}\,{M\over K}\, g\, \ell\big(2-\ell\big)}
\,;\quad \ell\in[\,0,\,1\,]\, .
\]
.
Falling speed of the top of the slinky coil
Consider a slinky coil in equilibrium whose top end is released and
starts to fall. Each part of the coil remains at rest until the top
end reaches there; at that moment it is incorporated into the falling
part and begins to fall together with it.
We derive how the falling speed of the top end changes with time
during this process.
At time $t$, let the top end have reached $\ell_{\rm top}(t)=i/N$ to
collapse and merge. Because the mass of the falling part is
$\ell_{\rm top}M$, the coordinate of the center‑of‑mass $z_G(t)$ at that
instant is
\begin{align}
z_G(t) & = {1\over M}\left(
\ell_{\rm top}M\, z^0(\ell_{\rm top})
+ \int_{\ell_{\rm top}}^1 d\ell' M\, z^0(\ell')\right)\\
& = -{1\over 2}\,{M\over K}\, g
\left({2\over 3} + \ell_{\rm top}^2 - {2\over 3}\ell_{\rm top}^3\right)\, .
\end{align}
The center of mass must fall with the uniform acceleration $-g$, thus
this should be
\[
z_G(t) = -{1\over 2}\, g t^2 + z_G^0 .
\]
Hence, the value of $\ell_{\rm top}$ at time $t$ is determined by
\[
\textcolor{blue}{
\ell_{\rm top}^2\left({1-{2\over 3}\,\ell_{\rm top}}\right)
= {K\over M}\; t^2
}.
\]
Using $\ell_{\rm top}(t)$ given by this equation, the position of the
top of the coil at time $t$ is
\[
\textcolor{green}{
z_{\rm top}(t) = z^0\big(\ell_{\rm top}(t)\big)
= -{1\over 2}\,{M\over K}\, g\,
\ell_{\rm top}(t)\big( 2-\ell_{\rm top}(t)\big)
} \tag{1}
\]
and its falling speed is
\begin{align}
v_{\rm top}(t) & = \dot z_{\rm top}
= {d z^0\over d\ell}\, \dot\ell_{\rm top}
=
-{M\over K}\,g\, \big( 1-\ell_{\rm top}\big)\,\dot\ell_{\rm top}\\
& = -g\sqrt{M\over K}\, \sqrt{1-{2\over 3}\ell_{\rm top}(t)}\; .
\end{align}
Note that these expressions are valid only for $\ell_{\rm
top}\in[0,1]$.
Thus, the initial falling speed of the top end at $t=0$ is obtained by
substituting $\ell_{\rm top}=0$ as
\[
\textcolor{blue}{
v_{\rm top}(0) = -g\sqrt{M\over K} \; .
} \tag{2}
\]
The top end, therefore, starts falling with a finite speed at $t=0$,
and the falling speed $v_{\rm top}$ actually decreases with time.
Wave speed along a spring under uniform tension $T$
Under a uniform tension $T$ without the gravity, the static
configuration of the coil is
\[
z_i^0 = \Delta z\times i\,; \qquad \Delta z = {T\over k}\; .
\]
Letting the displacement from this configuration be $\delta z_i$,
\[ z_i = z_i^0 + \delta z_i
\]
and assuming a wave with angular frequency $\omega$ and wavenumber $q$
\[
\delta z_i = C \sin(q\, i -\omega t)
\]
the dispersion relation becomes
\[
\omega^2 = {k\over m}\, 2(1-\cos q) \approx {k\over m}\, q^2
\qquad (q \approx 0)
\]
Hence, the wave speed along the spring with a zero‑natural‑length
under uniform tension $T$ is
\[
v(T) = \sqrt{k\over m}\, \Delta z(T) = {T\over\sqrt{MK}}
\]
In particular, when the tension equals the weight of the entire
spring, $T=Mg$,
\[
\textcolor{blue}{
v(Mg) = g\sqrt{M\over K} \; ,
} \tag{3}
\]
which coincides with the speed (2), namely
the initial speed of the top end of the falling coil.
Pulse propagation along a suspended slinky coil
In general, when a pulse is applied from outside to one end of a
linear spring in equilibrium at $t=0$, its influence reaches the
segment $i_p(t)$ at time $t$
\[
i_p(t) = \sqrt{k\over m}\times t .
\]
The corresponding $\ell_p(t)$ is
\[
\textcolor{blue}{
\ell_p(t) = {i_p(t)\over N} = \sqrt{K\over M}\; t,
} \]
which describes the propagation of the pulse. For a pulse applied to
the top of a vertically hanging slinky coil, the coordinate of the
leading edge of the pulse is
\[
\textcolor{green}{
z_p(t) = z^0\big(\ell_p(t)\big)
= -g\sqrt{M\over K}\; t \left( 1-{1\over 2}\sqrt{K\over M}\; t \right)
}\tag{4}
\]
The propagation speed $v_p(t)$ of the pulse is then
\begin{align}
v_p(t) & = {d z_p\over dt}
= -{M\over K}\, g\, \big( 1-\ell_p\big)\, \dot\ell_p\\
& = -g\left(\sqrt{M\over K} -t\right)
\end{align}
These expressions are valid only while the pulse has not yet reached the bottom end of the spring, i.e.,
\[
t < \sqrt{M\over K}
\]
.
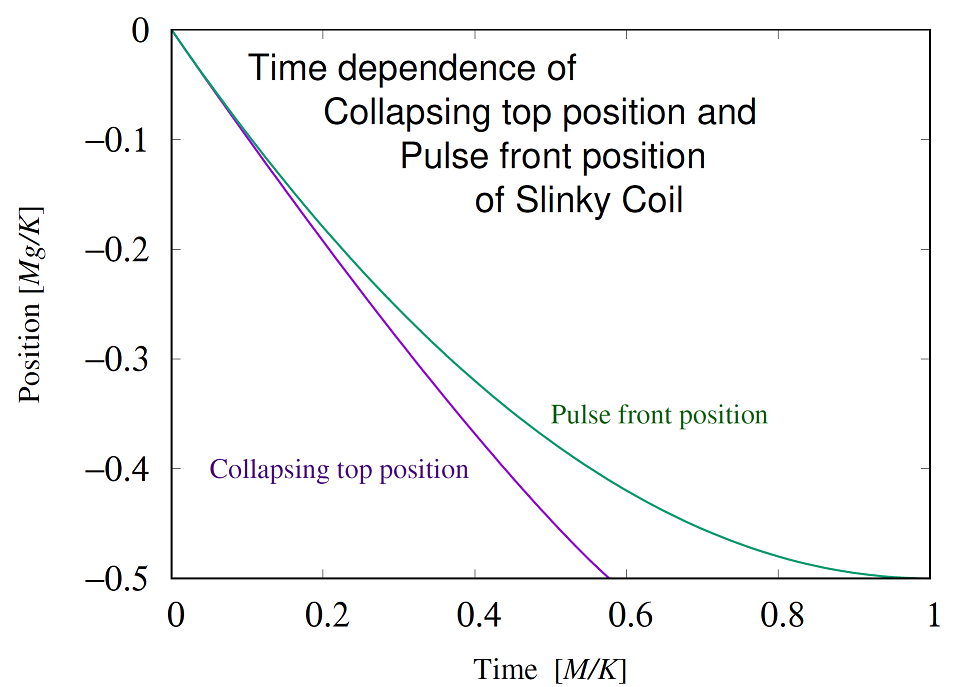
Graphs
Time evolution of the position of the collapsing top of a falling
slinky coil (1), and the position of the pulse front propagating along a
suspended slinky coil (4). Initially they move at the same speed, but
the collapsing top of the coil gradually gets ahead.