April 2024, Hiizu Nakanishi

We calculate the moment of inertia of an object consisting of two rods of length \( L \) and mass \( M/2 \) each, intersecting at an angle \( \theta \) at a point located \( L_1 \) from their midpoints.

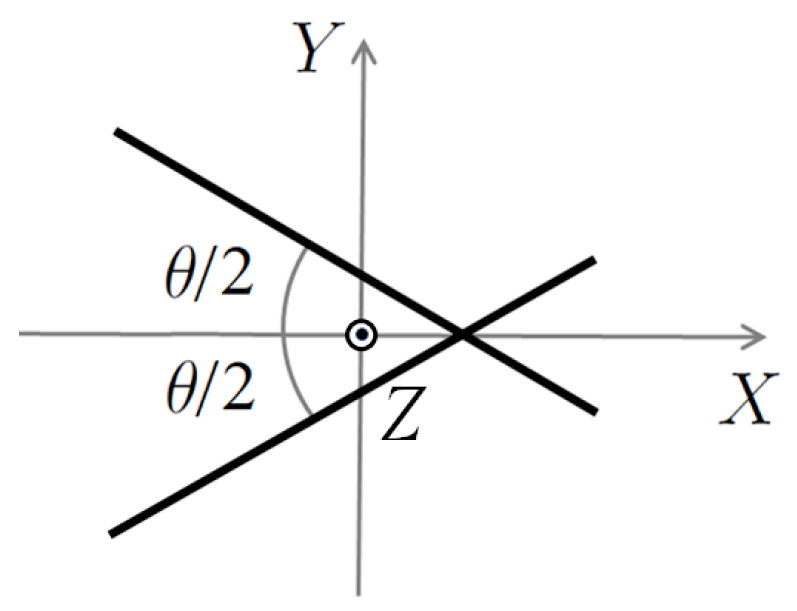
The linear mass density of the rods is given by:

\[ \rho := \frac{M}{2L} \]

Since the center of mass of the rods lies on the \( Y \)-axis, let the \( X \)-coordinates of the rod ends be \( \pm X_0 \), and the intersection point’s \( X \)-coordinate be \( X_1 \), then:

\[ X_0 := \frac{L}{2}\cos{\frac{\theta}{2}},\qquad X_1 := L_1\cos{\frac{\theta}{2}} \]

Each rod lies along:

\[ Y = \pm \tan{\frac{\theta}{2}}\, (X - X_1), \quad X \in [-X_0, X_0] \]

The moments \( I_X \), \( I_Y \), and \( I_Z \) are calculated as follows:

\[ \begin{align*} I_X &= 2\int_{-X_0}^{X_0} dX\; \rho\; \sqrt{1+\left(\frac{dY}{dX}\right)^2} \; Y^2 \\ &= \frac{1}{12} \left(1 + 12\left(\frac{L_1}{L}\right)^2\right) \sin^2\left(\frac{\theta}{2}\right) ML^2 \\ I_Y &= 2\int_{-X_0}^{X_0} dX\; \rho\; \sqrt{1+\left(\frac{dY}{dX}\right)^2} \; X^2 \\ &= \frac{1}{12}\cos^2\left(\frac{\theta}{2}\right) ML^2 \\ I_Z &= I_X + I_Y \\ &= \frac{1}{12} \left(1 + 12\left(\frac{L_1}{L}\right)^2 \sin^2\left(\frac{\theta}{2}\right)\right) ML^2 \end{align*} \]

The products \( I_{XZ} \) and \( I_{YZ} \) are zero because the mass of the object is distributed entirely in the \( XY \)-plane:

\[ I_{XZ} = I_{YZ} = 0 \]

For \( I_{XY} \), we use:

\[ I_{XY} = - \sum_{i=1}^N m_i X_i Y_i \]

However, since the mass distribution is symmetric with respect to the \( X \)-axis, for every mass point \( (X_i, Y_i, m_i) \), there is a corresponding point \( (X_i, -Y_i, m_i) \). Therefore:

\[ I_{XY} = -\sum_{i=1}^{N/2} \left(m_i X_i Y_i + m_i X_i (-Y_i)\right) = 0 \]

As all products of inertia are zero, the \( X \)-, \( Y \)-, and \( Z \)-axes are principal axes of inertia.