2024/4, Hiizu Nakanishi

長さ$L$、質量$M/2$の2つの棒が、中点から$L_1$のところで角度$\theta$で 交差した物体の慣性モーメントを計算する。

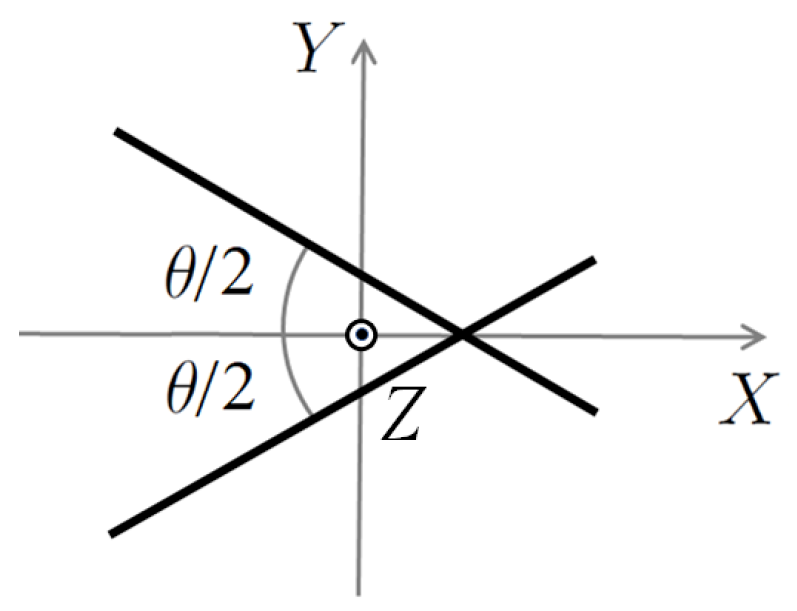
棒の線密度は$\displaystyle \rho:={M\over 2L}$で与えられる。

棒の重心は$Y$軸上にあるので、 棒の両端の$X$座標を$\pm X_0$、交差点の$X$座標を$X_1$とすると、 \[ X_0 := {L\over 2}\cos{\theta\over 2},\qquad X_1 := L_1\cos{\theta\over 2} \] である。それぞれの棒は、 \[ Y = \pm \tan{\theta\over 2}\,\big( X-X_1\big)\,; \quad X \in \big[-X_0, X_0\big] \] にある。

$I_X$, $I_Y$, $I_Z$は \begin{align*} I_X & = 2\int_{-X_0}^{X_0} dX\; \rho\; \sqrt{1+(dY/dX)^2}\; Y^2 % \\ % & = % 2 \rho \sqrt{1+\tan^2{\theta\over 2}}\, \tan^2{\theta\over 2} % \int_{-X_0}^{X_0} dX \big(X-X_1\big)^2 % \\ % & = % {1\over 3} \sqrt{1+\tan^2{\theta\over 2}}\, \tan^2{\theta\over 2} % \times % {M\over L}\left( \big(X_0-X_1\big)^3 + \big(X_0+X_1\big)^3 % \right) % \\ & = {1\over 12 }\left( 1 + 12 \left({L_1\over L}\right)^2\right) \sin^2{\theta\over 2}\; ML^2 \\ %------------------------- I_Y & = 2\int_{-X_0}^{X_0} dX\; \rho\; \sqrt{1+(dY/dX)^2}\; X^2 % \\ % & = 2\rho \sqrt{1+(dY/dX)^2} \int_{-X_0}^{X_0} dX \, X^2 % = % {2\over 3}\sqrt{1+\tan^2{\theta\over 2}}\, {M\over L}X_0^3 % \\ & = {1\over 12}\,\cos^2{\theta\over 2}\ ML^2 \\ %------------------------- I_Z & = I_X + I_Y = {1\over 12}\left( 1+ 12 \sin^2{\theta\over 2}\left({L_1\over L}\right)^2 \right) ML^2 \end{align*} と求められる。

$I_{XZ}$, $I_{YZ}$は、物体の質量が$XY$平面内に分布しているのでゼロ: \[ I_{XZ} = I_{YZ} = 0 \] $I_{XY}$は、 \[ I_{XY} = - \sum_{i=1}^N m_i X_i Y_i \] であるが、質量分布が$X$軸に対して対称なので、 質点$(X_i, Y_i, m_i)$に対して、 質点$(X_i, -Y_i, m_i)$が存在する。 そのため、 \[ I_{XY} =-\sum_{i=1}^{N/2}\Big( m_i X_i Y_i + m_i X_i \big(-Y_i\big)\Big) =0 \] が示される。

慣性乗積が全てゼロとなるので、 $X$, $Y$, $Z$軸は慣性主軸である。