2024/1/15, Hiizu Nakanishi

Kapitzaの振り子の理論

まず最初に、支点に加えられた振動が上下方向で \[ f(t) = f\sin(\Omega t) \] の場合を考える。

ラグランジアン

その場合、振子の重りの位置を$(x,y)$とすると、その位置と速度は \[\left\{\begin{array}{rl} x & = -\ell \sin\varphi \\ y & = \ell\cos\varphi + f(t) \end{array}\right. \hspace{5em} \left\{\begin{array}{rl} \dot x & = -\ell\dot\varphi \cos\varphi \\ \dot y & = -\ell\dot\varphi\sin\varphi + \dot f(t) \end{array}\right. \] で与えられ、ラグランジアンは \[ L = {1\over 2}m \Big( \ell^2\dot\varphi^2 -2\ell\dot\varphi\sin\varphi \dot f(t) +\dot f^2(t) \Big) - mg\big(\ell\cos\varphi + f(t)\big) \] となることがわかる。

運動方程式

ラグランジュの運動方程式は、 \[ {d p\over dt} = {\partial L\over\partial \varphi},\qquad p := {\partial L\over\partial\dot\varphi} = m\Big(\ell^2\dot\varphi -\ell\dot f(t)\sin\varphi\Big) \] $$ \Rightarrow\qquad \ddot\varphi = \left( \omega_0^2 + {\ddot f(t)\over\ell}\right)\sin\varphi \,;\qquad \omega_0:=\sqrt{g\over\ell} \tag{1} $$ と与えられる。以下では、 \[ f\ll\ell, \qquad \Omega\gg \omega_0 \] の場合を考える。

近似解

振子の角度$\varphi(t)$を、支点の振動と同じ大きな角速度 $\Omega$ で振動する成分 $\xi(t)$ と、ゆっくりとした運動の成分 $\Phi(t)$ に分けて、 \[ \varphi(t) = \Phi(t) + \xi(t) \tag{2} \] として、$\Phi(t)$ の従う方程式を導く。ここで $\xi(t)$ は $\Phi(t)$ よりもずっと小さく、振動の周期 $2\pi/\Omega$ で平均するとゼロとなるとする： \[ \xi(t)\ll\Phi(t), \qquad \overline{\xi(t)}:={\Omega\over 2\pi}\int_t^{t+2\pi/\Omega} \xi(t') dt'=0. \]

式(2)を式(1)に代入すると、 \begin{align*} \ddot\Phi(t) + \textcolor{red}{\ddot\xi(t) } & = \left( \omega_0^2 + {\ddot f(t)\over \ell}\right) \sin\big(\Phi(t)+\xi(t)\big) \\ & \approx \left( \omega_0^2 + \textcolor{red}{{\ddot f(t)\over \ell}}\right) \Big( \sin\Phi(t) + \textcolor{red}{\xi(t)\, \cos\Phi(t)} \Big). \tag{3} \end{align*} と近似できる。ここで $\Phi\ll\xi$ を用いた。

$\xi(t)$ と $f(t)$ は角振動数 $\Omega$ で振動しているとして、式(3)の中でこれらに関わる項の大きさを見積もると、 \[ \ddot\xi \sim \Omega^2\xi,\quad {\ddot f(t)\over\ell}\sin\Phi \sim \Omega^2{f\over\ell},\quad \omega_0^2\xi\cos\Phi\sim \omega_0^2\xi,\quad {\ddot f(t)\over\ell}\,\xi\cos\Phi \sim \Omega^2{f\over\ell}\,\xi \] となる。$\Omega\gg\omega_0,\; \xi\sim f/\ell$とすると、これらの項の大きさについて \[ \ddot\xi,\quad {\ddot f(t)\over\ell}\sin\Phi \qquad\gg\qquad \omega_0^2\xi\cos\Phi,\quad {\ddot f(t)\over\ell}\,\xi\cos\Phi \] という関係が得られる。これなの項のうち大きい２つの項が釣り合っているとして、 \[ \ddot\xi(t) = {\ddot f(t)\over\ell}\,\sin\Phi(t) \] とし、更に $\Phi(t)$ がゆっくり変化する変数であることに注意して \[ \xi(t)\approx {f(t)\over\ell}\,\sin\Phi(t) \] と近似する。これを式(3)に代入して振動の周期 $2\pi/\Omega$ で平均すると \begin{align*} \ddot\Phi(t) & = \omega_0^2 \sin\Phi(t) + \omega_0^2\,\overline{\xi(t)}\,\cos\Phi(t) + \overline{\ddot f(t) f(t)\over \ell^2}\sin\Phi(t)\cos\Phi(t) \\ & = \omega_0^2 \sin\Phi(t) - {\Omega^2f^2\over 2 \ell^2}\sin\Phi(t)\cos\Phi(t) \\ & := -{d\over d\Phi} U_{\rm eff}(\Phi) \tag{4} \end{align*} を得る。ここで、$\overline{\xi(t)}=0$を用いた。また、 $U_{\rm eff}(\Phi)$ は遅い変数 $\Phi$ に対する実効ポテンシャルで、 \[ U_{\rm eff}(\Phi):= \omega_0^2\cos\Phi + {\Omega^2 f^2\over 4\,\ell^2}\sin^2\Phi \tag{5} \] である。式(4)を単振り子の方程式の形に書き直すと \[ m\,{d\big(\ell\dot\Phi\big)\over dt} = -{d\over d(\ell\Phi)}\left( mg\ell\cos\Phi + \textcolor{red}{{1\over 2}m \overline{\big(\ell\dot\xi\,\big)^2 }} \right); \qquad \dot\xi(t) := {\Omega f(t)\over\ell}\sin\Phi \] となり、実効ポテンシャルの第２項は外力による振動の運動エネルギーの時間平均と解釈できることがわかる。

式(5)を $\Phi$ で展開すると、 \[ U_{\rm eff} (\Phi) = \omega_0^2\left[ 1 +{1\over 2}\left( -1 + {1\over 2}\left({\Omega f\over\omega_0\ell}\right)^2\right)\Phi^2 + O\big(\Phi^4\big)\right] \] となるので、 \[ f\,\Omega > \sqrt 2\; \ell\,\omega_0 \] で倒立状態 $\Phi=0$ が安定となる。

外部振動の向きが角度 $\theta$ 傾いているとき

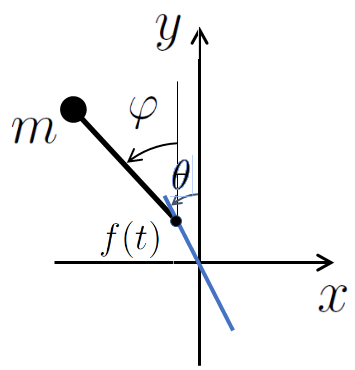同様の解析をすると、実効ポテンシャルとして \[ U_{\rm eff}(\Phi) = \omega_0^2\cos\Phi + {\Omega^2 f^2\over 4\,\ell^2}\sin^2\big(\Phi-\theta\big) \] を得る。この外部振動によるポテンシャルは $\theta$ および $\theta+\pi$ 方向で最小となることがわかる。