

| : Display | |
| Rotation around $z$-axis: | $\phi=$ 0° | |
| Rotation around $x'$-axis: | $\theta=$ 0° | |
| Rotation around $z''$-axis: | $\psi=$ 0° |
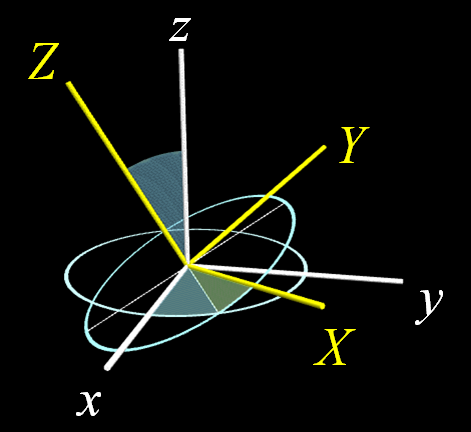
The original $xyz$ coordinate system is shown by the white axes.
The $XYZ$ system obtained by rotation using Euler angles is shown by
the yellow axes.
| Rotate $xyz$ system | around $z$-axis | by angle $\phi$ to obtain | $x'y'z'$ system |
| Rotate $x'y'z'$ system | around $x'$-axis | by angle $\theta$ to obtain | $x''y''z''$ system |
| Rotate $x''y''z''$ system | around $z''$-axis | by angle $\psi$ to obtain | $XYZ$ system |
Rotation Matrix $R(\phi,\theta,\psi)$:
Let a vector $\vec a$ have components \[ \vec a^S = \begin{pmatrix} a_x \\ a_y \\ a_z \end{pmatrix}, \quad \mbox{and}\quad \vec a^B = \begin{pmatrix} a_X \\ a_Y \\ a_Z \end{pmatrix} \] in the $xyz$ system and $XYZ$ system, respectively.
The relationship between these representations is given by \[ \vec a^S = R(\phi,\theta,\psi)\vec a^B , \] where the rotation matrix $R$ is defined as \[ R = R(\phi,\vec{n}_3) R(\theta,\vec{n}_1) R(\psi,\vec{n}_3). \] Here, the rotation matrix $R(\phi, \vec n)$ represents the rotation by the angle $\phi$ around the axis $\vec n$: \[\small {\rm R}(\phi,{\vec n}_3):= \left(\begin{array}{ccc} \cos\phi, & -\sin\phi, & 0 \\ \sin\phi, & \cos\phi, & 0 \\ 0, & 0, & 1 \end{array} \right),\quad % {\rm R}(\theta,{\vec n}_1):= \left(\begin{array}{ccc} 1,&0,& 0\\ 0, & \cos\theta, & -\sin\theta \\ 0, & \sin\theta, & \cos\theta \end{array} \right),\quad % {\rm R}(\psi,{\vec n}_3):= \left(\begin{array}{ccc} \cos\psi, & -\sin\psi, & 0 \\ \sin\psi, & \cos\psi, & 0 \\ 0, & 0, & 1 \end{array} \right). \]
Thus, we obtain the rotation matrix for the rotation by Euler angles \[ R(\phi,\theta,\psi) = \begin{pmatrix} \cos\phi\cos\psi - \sin\phi\cos\theta\sin\psi & -\cos\phi\sin\psi - \sin\phi\cos\theta\cos\psi & \sin\phi\sin\theta \\ \sin\phi\cos\psi + \cos\phi\cos\theta\sin\psi & -\sin\phi\sin\psi + \cos\phi\cos\theta\cos\psi & -\cos\phi\sin\theta \\ \sin\theta\sin\psi & \sin\theta\cos\psi & \cos\theta \end{pmatrix} \]
Angular Velocity Vector $\vec{\omega}$:
When $(\phi,\theta,\psi)$ are functions of time, the angular velocity vector of $XYZ$ system relative to $xyz$ system is \[ \vec{\omega} = \dot{\phi}\vec{e}_z + \dot{\theta}\vec{e}_{x'} + \dot{\psi}\vec{e}_Z \] with \[ \vec{e}_z = \sin\theta\sin\psi\vec{e}_X + \sin\theta\cos\psi\vec{e}_Y + \cos\theta\vec{e}_Z, \quad \vec{e}_{x'} = \cos\psi\vec{e}_X - \sin\psi\vec{e}_Y \] Thus, we get \[ \begin{aligned} \omega_X &= \dot{\phi}\sin\theta\sin\psi + \dot{\theta}\cos\psi, \\ \omega_Y &= \dot{\phi}\sin\theta\cos\psi - \dot{\theta}\sin\psi, \\ \omega_Z &= \dot{\phi}\cos\theta + \dot{\psi}. \end{aligned} \] Solving inversely \[ \begin{aligned} \dot{\phi} &= \frac{1}{\sin\theta}(\sin\psi\,\omega_X + \cos\psi\,\omega_Y), \\ \dot{\theta} &= \cos\psi\,\omega_X - \sin\psi\,\omega_Y, \\ \dot{\psi} &= -\frac{1}{\tan\theta}(\sin\psi\,\omega_X + \cos\psi\,\omega_Y) + \omega_Z. \end{aligned} \]
Note that these equations are singular at $\theta = 0$, so numerical integration using Euler angles may become inaccurate near this singularity.