

| : 表示 | |
| $z$ 軸周りの回転角: | $\phi=$ 0° | |
| $x'$ 軸周りの回転角: | $\theta=$ 0° | |
| $z''$ 軸周りの回転角: | $\psi=$ 0° |
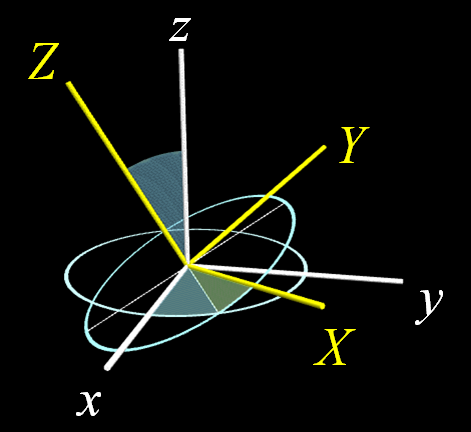
元の$xyz$座標系を白で表し、
それをオイラー角$(\phi,\theta,\psi)$で回転した$XYZ$座標系を
黄色で表している。
| $xyz$系を | $z$軸周りに | 角度$\phi$ 回転した座標系を | $x'y'z'$系 |
| $x'y'z'$系を | $x'$軸周りに | 角度$\theta$ 回転した座標系を | $x''y''z''$系 |
| $x''y''z''$系を | $z''$軸周りに | 角度$\psi$ 回転した座標系を | $XYZ$系 |
回転行列$R(\phi,\theta,\psi)$: 任意のベクトル $\vec a$ の $xyz$ 系での成分と $XYZ$ 系での成分 \[ \vec a^S:=\left(\begin{array}{c}a_x \\ a_y \\ a_z\end{array}\right), \qquad \vec a^B:=\left(\begin{array}{c}a_X \\ a_Y \\ a_X\end{array}\right), \] の間の関係、すなわち 座標変換 \[ \vec a^S = R(\phi,\theta,\psi)\,\vec a^B \] を表す回転行列 $R(\phi,\theta,\psi)$は 1軸 $\vec n_1:=(1,0,0)$と3軸 $\vec n_3:=(0,0,1)$の周りの回転行列 \[\small {\rm R}(\phi,{\vec n}_3):= \left(\begin{array}{ccc} \cos\phi, & -\sin\phi, & 0 \\ \sin\phi, & \cos\phi, & 0 \\ 0, & 0, & 1 \end{array} \right),\quad % {\rm R}(\theta,{\vec n}_1):= \left(\begin{array}{ccc} 1,&0,& 0\\ 0, & \cos\theta, & -\sin\theta \\ 0, & \sin\theta, & \cos\theta \end{array} \right),\quad % {\rm R}(\psi,{\vec n}_3):= \left(\begin{array}{ccc} \cos\psi, & -\sin\psi, & 0 \\ \sin\psi, & \cos\psi, & 0 \\ 0, & 0, & 1 \end{array} \right) \] を用いて \[ R(\phi,\theta,\psi) = R(\phi,\vec n_3) R(\theta,\vec n_1) R(\psi,\vec n_3) \] と表される。これより、 \[ R(\phi,\theta,\psi) =\left(\begin{array}{ccc} \cos\phi\cos\psi-\sin\phi\cos\theta\sin\psi, & -\cos\phi\sin\psi-\sin\phi\cos\theta\cos\psi, & \sin\phi\sin\theta \\ \sin\phi\cos\psi+\cos\phi\cos\theta\sin\psi, & -\sin\phi\sin\psi+\cos\phi\cos\theta\cos\psi, & -\cos\phi\sin\theta \\ \sin\theta\sin\psi, & \sin\theta\cos\psi, & \cos\theta \end{array} \right) \] と求められる。
$XYZ$ 系の回転の角速度ベクトル $\vec\omega$と $(\dot\phi,\dot\theta,\dot\psi)$の関係: 角度$(\phi,\theta,\psi)$が時間変化しているときの$XYZ$ 系の $xyz$系に対する回転の角速度ベクトル $\vec\omega$ は \[ \vec\omega = \dot\phi\,\vec e_z + \dot\theta\,\vec e_{x'} + \dot\psi\,\vec e_{Z} \] で与えられる。ただし、$\vec e_z$, $\vec e_{x'}$, $\vec e_Z$は、 それぞれ $z$軸、$x'$軸、$Z$軸方向の単位ベクトルで、 \[ \vec e_z = \sin\theta\sin\psi\,\vec e_X +\sin\theta\cos\psi\,\vec e_Y +\cos\theta\,\vec e_Z, \qquad \vec e_{x'} = \cos\psi\,\vec e_X -\sin\psi\,\vec e_Y \] なので、 \begin{eqnarray} \omega_X & = & \dot\phi\sin\theta\sin\psi + \dot\theta\cos\psi, \\ \omega_Y & = & \dot\phi\sin\theta\cos\psi - \dot\theta\sin\psi, \\ \omega_Z & = & \dot\phi\cos\theta + \dot\psi \end{eqnarray} が得られる。 これを逆に解くことにより、$(\dot\phi,\dot\theta,\dot\psi)$は $(\omega_X, \omega_Y, \omega_Z)$を用いて \begin{eqnarray} \dot\phi & = & {1\over\sin\theta}\big( \sin\psi\,\omega_X + \cos\psi\,\omega_Y\big), \\ \dot\theta & = & \cos\psi\,\omega_X - \sin\psi\,\omega_Y, \\ \dot\psi & = & -{1\over\tan\theta}\big( \sin\psi\,\omega_X + \cos\psi\,\omega_Y\big) + \omega_Z \end{eqnarray} と表される。
この関係式には $\theta=0$ に特異点があるので、この式を用いて、 角速度 $(\omega_Z,\omega_Y,\omega_Z)$ から オイラー角 $(\phi,\theta,\psi)$ を数値積分で求めると、 特異点近傍で精度が落ちる。